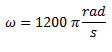gala
Atias
CIRCUITO RLC
En electrodinámica un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina (inductancia) y un condensador (capacitancia).
Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describe generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primer orden).
Con ayuda de un generador de señales, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento de la corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencial que lo rige).
Circuito RLC en serie
Dibujamos el diagrama de vectores teniendo en cuenta:
-
que la intensidad que pasa por todos los elementos es la misma,
-
que la suma (vectorial) de las diferencias de potencial entre los extremos de los tres elementos nos da la diferencia de potencial en el generador de corriente alterna.
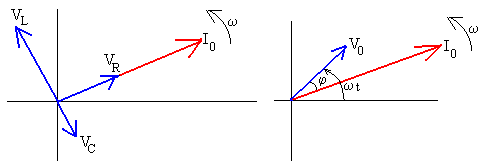

El vector resultante de la suma de los tres vectores es
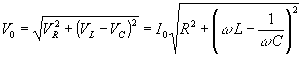
Se denomina impedancia del circuito al término
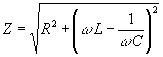
de modo que se cumpla una relación análoga a la de los circuitos de corriente continua
V0=I0·Z.
El ángulo que forma el vector resultante de longitud V0 con el vector que representa la intensidad I0 es
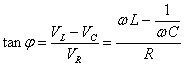
Las expresiones de la fem y de la intensidad del circuito son
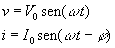
Ejemplo:
-
R=1.5 Ω
-
L=5·10-3 H
-
C=4·10-6 F
-
ω=1.01·w0
La frecuencia propia del circuito es
La frecuencia del generador es ω=1.01·w0=7142 rad/s
La impedancia vale
El desfase es
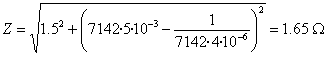
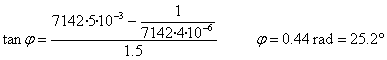
Resonancia en un circuito LCR en serie
La condición de resonancia la estudiamos en las oscilaciones forzadas de una masa unida a un muelle elástico.
La potencia suministrada por el generador de corriente alterna es
P=i·v=V0·I0sen(w t)·sen(w t-j )
P=V0·I0sen(w t)·(sen(w t)·cos j - cos(w t)·senj)=V0·I0(sen2(w t)·cos j - sen(wt)·cos(w t)·senj)
Esta magnitud es una función complicada del tiempo que no es útil desde el punto de vista práctico. Lo que tiene interés es el promedio de la potencia en un periodo 2p /w .
<P>=V0·I0(<sen2(w t)>·cos j - <sen(w t)·cos(w t)>·senj)
Se define como valor medio <f(t)> de una función periódica f(t) de periodo T a la integral
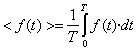
El periodo de la función f(t)=sen2(w t) es T=π/ω, su valor medio es
<sen2(w t)>=1/2
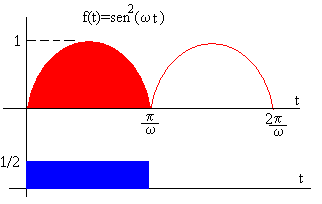
El área de color rojo es igual al área de color azul.
El periodo de la función f(t)=sen(w t)·cos(w t)=sen(2w t)/2 es T=π/ω, su valor medio es
<sen(w t)·cos(w t)>=0
como puede comprobarse fácilmente
El valor medio de la energía por unidad de tiempo, o potencia suministrada por el generador es
Ejercicio 1
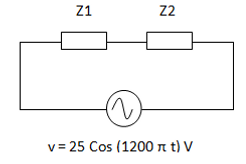
Hallar la corriente total que circula por el siguiente circuito. Expresarla con una función coseno.
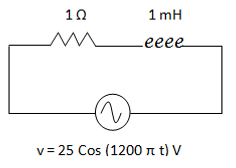
Reemplazando por impedancias nos queda un circuito con la siguiente forma:
Obtenemos primero la velocidad angular de la fuente a partir de su expresión de tensión
.
La impedancia de la resistencia es igual a su valor y no tiene parte imaginaria.
Para calcular Z2 hallamos primero la reactancia inductiva.
Z2 no tiene parte real y solo está formada por la reactancia inductiva en su parte imaginaria.
Calculamos Z12 como la asociación en serie de Z1 y Z2. Debido a que no hay otras impedancias, ésta ya es la impedancia total.
Convertimos la tensión de la fuente a forma fasorial. Como luego debemos obtener una expresión en función del tiempo, utilizamos directamente el valor máximo de tensión como módulo del fasor. Debido a que no hay ángulo de fase, el ángulo del fasor es 0°.
Pasamos la impedancia a forma polar.
Planteamos la ley de Ohm.
Escribimos la corriente con una función coseno a partir del fasor de corriente hallado.